DISTRIBUCIÓN DE LAS CARGAS DEL POTENCIAL ELÉCTRICO ANTE UN CUERPO CONDUCTIVO Y UNO RESISTIVO
INTRODUCCIÓN
La Electrodinámica es una parte de la Física enfocada a la electricidad cuyo principal objetivo es estudiar las cargas eléctricas en movimiento a través de los conductores. El término corriente eléctrica se emplea para describir la rapidez de flujo de carga que pasa por alguna región del espacio, este flujo de carga se ve afectado por la resistencia o conductividad del material o bien por materia que encuentra a su paso. esta razón de cambio en la transferencia de energía de una corriente eléctrica es la potencia, por lo que cuando realizamos levantamientos de prospección eléctrica nuestros mapas son realizados aprovechando esta diferencia de potencial. En la siguiente investigación se presenta una recopilación de información con el objetivo de comprender como es este comportamiento en los materiales conductores y resistivos.
OBJETIVOS
Conocer como es el comportamiento de un cuerpo conductivo y uno resistivo a través del potencial eléctrico.
DESARROLLO
Es el trabajo que debe realizar un campo electrostático para mover una carga positiva desde dicho punto hasta el punto de referencia, dividid
o por unidad de carga de prueba. Dicho de otra forma, es el trabajo que debe realizar una fuerza externa para traer una carga positiva unitaria q desde el punto de referencia hasta el punto considerado en contra de la fuerza eléctrica a velocidad constante. Matemáticamente se expresa por:
CONCEPTOS BÁSICOS
Flujo de carga eléctrica:
En electromagnetismo el flujo eléctrico, o flujo electrostático,1 es una cantidad escalar que expresa una medida del campo eléctrico que atraviesa una determinada superficie,2 o expresado de otra forma, es la medida del número de líneas de campo eléctrico que penetran una superficie. Su cálculo para superficies cerradas se realiza aplicando la ley de gauss. Por definición el flujo eléctrico parte de las cargas positivas y termina en las negativas, y en ausencia de las últimas termina en el infinito.
Para que exista una corriente eléctrica es necesario que las cargas eléctricas estén sometidas a un campo eléctrico, de tal manera que éste origine la fuerza necesaria para que las cargas adquieran un movimiento definido. La carga fluye cuando hay una diferencia de potencial entre los extremos de un conductor. Cuando en los extremos de un conductor de electricidad están a potenciales eléctricos distintos, se inicia un flujo de carga que va del extremo de mayor potencial al de menor potencial.
Corriente eléctrica
Lo que conocemos como corriente eléctrica no es otra cosa que la circulación de cargas o electrones a través de un circuito eléctrico cerrado, que se mueven siempre del polo negativo al polo positivo de la fuente de suministro de fuerza electromotriz (FEM).
|
Un material conductor es aquel que permite el transporte de carga eléctrica. En general, los sólidos metálicos son buenos conductores, ya que sus electrones de valencia están poco ligados a los núcleos atómicos, lo que permite que se muevan con facilidad a través del sólido. Este tipo de electrones poco ligados se denominan electrones libres.
Cuando a un sólido conductor cargado con una cierta carga q, se le deja evolucionar la suficiente cantidad de tiempo, alcanza una situación de equilibrio electrostático en la que ya no hay movimiento de cargas. En estas condiciones, el campo en el interior del conductor es nulo (si no, habría movimiento de cargas y no estaría en equilibro).
Esta distribución de carga dentro del conductor genera un campo eléctrico interno de sentido opuesto al externo y de igual módulo, de modo que en el interior del conductor el campo eléctrico total es nulo. Este hecho constituye en principio de funcionamiento de una jaula de Faraday. En la sección "Sabías que..." encontrarás una explicación de cómo funciona.
Si el campo en el interior de un material conductor en equilibrio electrostático es nulo, no puede haber carga eléctrica en el interior del mismo. Por tanto, la carga de un conductor se acumula en su superficie.
El campo eléctrico externo al conductor no puede tener componente tangencial, ya que las cargas de la superficie se moverían sobre ella y ya no sería un conductor en equilibrio; es decir, el campo externo es normal a la superficie del conductor.
Propiedades de los conductores en equilibrio electrostático
Las propiedades de los conductores en equilibrio electrostático se pueden resumir en:
- El campo eléctrico en el interior es nulo.
- La carga eléctrica se distribuye sobre la superficie, concentrándose en las zonas de menor radio de curvatura (es decir, más puntiagudas).
- La superficie del conductor es una superficie equipotencial.
- El campo eléctrico en la superficie está dirigido hacia afuera y es perpendicular a la superficie.
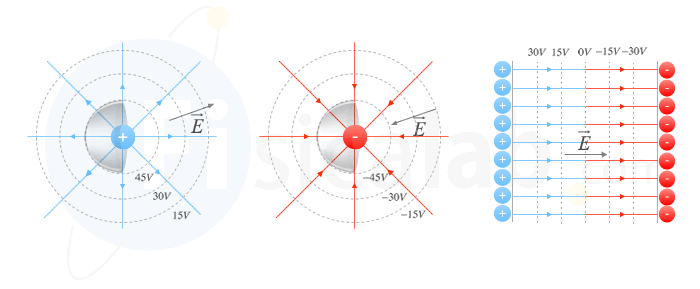
- DISTRIBUCIÓN DE LAS CARGAS DEL POTENCIAL ELÉCTRICO EN CUERPOS CONDUCTIVOS Y RESISTIVOSCuando se está en presencia de variaciones más o menos locales de resistividad, un cuerpo conductor por ejemplo atraerá y concentrará las líneas de corriente, en cambio las lineas equipotenciales serán repelidas por el conductor.Inversamente para un cuerpo resistivo, las lineas de corriente tendrán tendencia a bordear los obstáculos resistivos, mientras que las equipotenciales se estrecharán en la proximidad y en el interior de este cuerpo.
Desafortunadamente, los efectos de estas heterogeneidades locales se atenúan muy rápidamente con la distancia. Por tanto, es dificil poner en evidencia la existencia del cuerpo anómalo cuando su profundidad es del mismo orden de mágnitud que las dimensiones del cuerpo perturbador.Los minerales semiconductores son muchos y de gran importancia práctica. Su resistividad depende de su contenido en impurezas, a veces en grado extremo. Además su conductividad aumenta con la temperatura. Por ello, no cabe esperar que la resistividad de una especie mineralógica determinada pueda representarse por un dato único, sino que puede variar dentro de límites amplios. En general los teluros y los arseniuros son conductores muy buenos. Los sulfuros suelen entrar también entre los conductores buenos, con excepciones como la blenda y el cinabrio. Los óxidos, y los compuestos de antimonio suelen ser malos conductores, con la excepción de la magnetita. Ahora bien, estos minerales no suelen aparecer en la naturaleza de forma individual, sino en asociaciones, y junto con una ganga frecuentemente aislante (cuarzo, calcita, etc.), por lo que la resistividad conjunta del filón puede variar mucho de unos casos a otros. En los cuerpos dieléctricos o aisladores, los electrones están fuertemente ligados a l Esto puede deberse a que existan enlaces covalentes o iónicos. En este último caso la red cristalina forma un electrólito sólido. La mayoría de los minerales pertenecen a este grupo. A temperaturas normales las resistividades son muy altas, generalmente superiores a 10ˆ7 Wm. Son minerales dieléctricos el azufre, la blenda, la calcita, el cinabrio, el cuarzo, las micas y el petróleo entre otros. Entre estos minerales, además, figuran los más importantes constituyentes de las rocas, las cuales se comportarían como aisladoras si no fuera por la presencia de electrolitos.Si la resistividad de las rocas dependiese únicamente de los minerales constituyentes, habrían de considerarse como aislantes en la inmensa mayoría de los casos, puesto que el cuarzo, los silicatos, la calcita, las sales, etc., lo son prácticamente. Sólo en el caso de que la roca contuviese minerales semiconductores en cantidad apreciable, podría considerarse como conductora, es decir, sólo lo serían las menas metálicas. Afortunadamente, todas las rocas tienen poros en proporción mayor o menor, los cuales suelen estar ocupados total o parcialmente por electrolitos, de lo que resulta que, en conjunto, las rocas se comportan como conductores iónicos, de resistividad muy variable según los casos. La resistividad de las rocas puede variar en margen amplísimo en función del contenido en agua, de la salinidad de ésta y del modo de distribución de los poros.
La resistividad de las rocas también depende de la temperatura a la que se encuentre ya que la temperatura influye notablemente en la resistividad de los fluidos que hay en los poros. En concreto, un descenso de la temperatura provoca un aumento de la resistividad y en el punto de congelación el agua pasa a ser un dieléctrico mal conductor. Por último, cabe mencionar que la resistividad de algunos minerales, y como consecuencia de las rocas que estos forman, varía según la dirección de medida que se toma, es decir, que presentan anisotropía. La formación de estratos puede producir anisotropía. Tal es el caso de las rocas sedimentarias. En general este efecto será débil dada la aleatoriedad de las orientaciones de los minerales en la roca.
como ingenieros en geociencias es importante conocer el comportamiento de el flujo de las cargas eléctricas en materiales conductivos y resistivos para exploraciones electricas pues a partir de ello podremos interpretar la resistivdad del terreno cuando realicemos un levantamiento eléctrico, ademas nos sera útil para determinar el diseño de la conexión a tierra de instalaciones nuevas siendo ideal encontrar un lugar con la menor resistencia posible para obtener mejores resultados del levantamiento.