Jose de Jesus Torres s.: marzo 2017

Principios básicos de la probabilidad

INTRODUCCIÓN

La importancia de la probabilidad radica en que, mediante este recurso matemático, es posible ajustar de la manera más exacta posible los imponderables debidos al azar en los más variados campos tanto de la ciencia como de la vida cotidiana.

En efecto, la probabilidad es una estrategia mediante la cual se intenta estimar la frecuencia con la que se obtiene un cierto resultado en el marco de una experiencia en la que se conocen todos los resultados posibles. Así, el ejemplo más tradicional consiste en definir cual es la pre valencia de obtener un número al arrojar un dado. Sobre seis resultados posibles (todas las caras), sólo es posible lograr un número por cada vez que el dado es arrojado. En este caso, la probabilidad puede expresarse como uno en seis, un sexto, la sexta parte o, en términos matemáticos precisos, 0.16 ó 16%.
La teoría de la probabilidad, en especial en el marco de sistemas más complejos, se aplica en áreas variadas del conocimiento, como las ciencias exactas (estadística, matemática pura y aplicada, física, química, astronomía), las ciencias sociales (sociología, psicología social, economía), la astronomía, la meteorología y, en especial en forma más reciente, la biomedicina.

La importancia esencial de la aplicación de los métodos de cálculo de la probabilidad reside en su capacidad para estimar o predecir eventos. Cuanto mayor sea la cantidad de datos disponibles para calcular la probabilidad de un acontecimiento, más preciso será el resultado calculado. Dada la complejidad de los sistemas en los que suele aplicarse la teoría de la probabilidad, se requiere de modelos informáticos y estadísticos de gran elaboración, que serían imposibles de no contarse con los modernos recursos tecnológicos relacionados con la computación.

Un buen ejemplo de su aplicabilidad cotidiana lo constituyen los análisis del comercio de las commodities (materias primas) en las relaciones internacionales actuales. Dado que gran parte de los factores involucrados en la estimación de la producción son azarosos (vientos, humedad ambiental, exposición solar, mano de obra real, condiciones económicas y financieras locales, avatares políticos regionales, entre otros), la teoría de la probabilidad resulta de gran importancia, ya que intenta ajustar en conceptos matemáticos cual será el devenir de los acontecimientos para calcular, por ejemplo, la producción final de cereales, combustibles fósiles y otros recursos de un área geográfica.

Por lo tanto, la probabilidad es una herramienta fundamental en la planificación estratégica de los movimientos sociales, económicos y laborales de toda la comunidad. Para esto es importante saber los siguientes términos.

Probabilidad: La probabilidad es la oportunidad de que algo pueda suceder. Un evento es una o más de las respuestas de que suceda ese algo.

Experimento: la actividad que produce eventos.

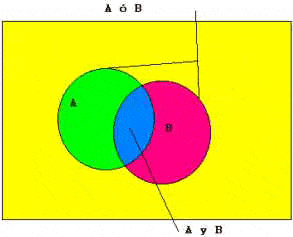
Evento mutuamente excluyente:Son aquellos eventos en los que se cumple la característica de que NO pueden suceder al mismo tiempo.

Evento no mutuamente excluyente:

Son aquellos eventos que PUEDEN suceder a un MISMO TIEMPO.

EQUIPROBABILIDAD:
El concepto de equiprobabilidad sugiere que si no hay razón para favorecer una ninguno de los posibles resultados de un experimento, entonces los resultados deben ser considerados IGUALMENTE PROBABLES de ocurrir.

P(águila) = P (sol)

FÓRMULA DE PROBABILIDAD MARGINAL:

P(EVENTO) = NÚMERO DE CASOS FAVORABLES PARA EL EVENTO / NÚMERO TOTAL DE RESULTADOS DEL EXPERIMENTO.

Ejemplo: ¿ Cuál es la probabilidad que en un tiro de una moneda aparezca águila?

P(águila) = 1 (¿Cuántas águilas pueden caer en ese tiro?) / 2 (¿Cuántos lados o caras tiene la moneda?).

P(águila) = ½ = 0.5 = 50% la probabilidad se puede expresar en decimales, porcentajes o fracciones.

Veamos el ejemplo en un dado.
El espacio muestral será de :
S= 1,2,3,4,5,6

¿Cuál es la probabilidad de que caiga un número par de ese dado?
Seleccionemos los pares.
S= 1,2,3,4,5,6

Tenemos que la probabilidad es:
P(pares dado) = 3 (tres número que son pares, por lo tanto hay tres posibilidades de que sea par) / 6 (el número de elementos de mi espacio)

P(pares dado) = 3/6 = 0.5 = 50%

¿Cuál es la probabilidad de que caiga el número 3 de ese dado?

P(# 3) = 1 (en el dado sólo existe un número 3) / 6 (total de elementos de mi espacio)

P(# 3) = 1/6 = 0.16 = 16%.

PROBABILIDAD BAJO CONDICIONES DE INDEPENDENCIA ESTADÍSTICA.
Cuando ocurren dos eventos el resultado del primero PUEDE O NÓ tener un efecto en el resultado del segundo evento, es decir, los eventos pueden ser tanto dependientes o independientes.

EVENTOS ESTADÍSTICAMENTE INDEPENDIENTES.
Son aquellos en los cuales la ocurrencia de un evento NO tiene efecto en la probabilidad de la ocurrencia de cualquier otro evento.

Existen 3 tipos de probabilidad bajo la condición de independencia estadística:

Marginal: Probabilidad individual significa que sólo puede tener lugar un evento.

P(SOL) = ½

Conjunta: Es la probabilidad de que 2 o más eventos independientes ocurran junto o en sucesión, es el producto de sus probabilidades marginales.

Fórmula :

P(AÇB) = P(A) * P(B)
P(AÇB) = PROBABILIDAD DE QUE LOS EVENTOS A Y B OCURRAN JUNTOS O EN SUCESIÓN.
P(A) = PROBABILIDAD MARGINAL DE A.
P(B) = PROBABILIDAD MARGINAL DE B.

Ejemplo: Si lanzamos 2 veces una moneda, ¿cuál es la probabilidad de obtener 2 águilas (águila y águila)?
S= Moneda 1 águila, sol.
Moneda 2 águila, sol.

P(águila) P(águila) * P (águila) = ½ * ½ = ¼

Condicional:
Es aquella en la cual la probabilidad de un evento se encuentra condicionada a la ocurrencia de otro evento.

P( B½A) = P( B)
Se lee : “ la probabilidad del evento B si el evento ha ocurrido”.

En el siguiente videocurso (Educatina) se hace una breve introducción al concepto de probabilidad, aprenderás cómo se calcula la probabilidad y otros conceptos básicos.

HISTORIA DE LA PROBABILIDAD

¿Qué indica la probabilidad? El cálculo matemático de probabilidades se basa en situaciones teóricas en las cuales puede configurarse un espacio muestral cuyos sucesos elementales tengan todos la misma probabilidad. La probabilidad de un resultado se representa con un número entre 0 y 1 : la probabilidad 0 indica que el resultado no ocurrirá nunca, y la probabilidad 1, que el resultado ocurrirá siempre. 4
5. Modelos de probabilidad De Frecuencia Relativa , a posteriori o empírico Utiliza la observación de datos, registrando su frecuencia de ocurrencia y usando esta información para pronosticar la posibilidad de una nueva ocurrencia. Subjetivo o intuitivo Se basa en la mejor conjetura con base a la evidencia disponible. Se aplica para eventos nuevos. Clásico , a priori o de Laplace Sirve para determinar la probabilidad de un hecho antes de que ocurra , mediante su cálculo teórico , con base a resultados igualmente probables. 5
6. Modelo de frecuencia relativa Si un experimento bien definido se repite n veces (n grande); sea nA < n el número de veces que el evento A ocurre en los n ensayos, entonces la frecuencia relativa de veces que ocurre el evento A “nA /n”, es la estimación de la probabilidad que ocurra el evento A : P(A)= nA /nOBSERVACIONES:1. La frecuencia relativa de un evento, esta comprendido entre 0 y 1. Por lo tanto 0 ≤ P(A) ≤ 1.En efecto: Desde que 0 ≤ nA ≤ 1, 0/n ≤ nA /n ≤ 1, se tiene que 0 ≤nA /n ≤ 1. Luego, 0 ≤ P(A) ≤ 1.2. nA /n = 0, si solo si, en las n repeticiones del experimento el evento A.6
7. Modelo SubjetivoDice que la probabilidad de ocurrencia de un evento esel grado de creencia por parte de un individuo de que unevento ocurra, basado en toda la evidencia a sudisposición.Bajo esta premisa se puede decir que este enfoque esadecuado cuando solo hay una oportunidad de ocurrenciadel evento y cuando no se cuenta con ninguna evidencia.Puede ser muy acertado o muy desligado de la realidad ,pues es un juicio personal. 7
8. Modelo ClásicoLa probabilidad de un evento es la razón entre elnúmero de casos (sucesos) favorables y el numero totalde casos (sucesos) posibles, siempre que nada obligue acreer que algunos de estos sucesos debe tenerpreferencia a los demás, lo que hace que seanigualmente posibles.La probabilidad de un evento A: P (A), es un NÚMERO,que mide el grado de certeza en el que un evento Aocurre, y se obtiene con la formula conocida comoREGLA DE LAPLACE: 8
9. Espacio Muestral y EventoCada experimento aleatorio tiene varios resultadosposibles y podemos describir con precisión elconjunto de estos resultados posibles. LlamaremosEspacio Muestral asociado a un experimentoaleatorio, al conjunto de todos los resultadosposibles de dicho experimento aleatorio, y lodenotamos con Ω.A uno o más de los resultados posibles del espaciomuestral, se les denomina Evento o Suceso, y sesimboliza con las letras mayúsculas: A, B, C, … Es un subconjunto del espacio muestral. 9
10. Tipos de EventosElemental :A cada elemento o resultado posible delespacio muestral, se le conoce con el nombre de eventoelemental.Imposible :Algunos eventos nunca pueden ocurrir en elexperimento aleatorio, y por eso se llama imposible. Sesimboliza con Ø.Seguro :Los eventos que siempre suceden en elexperimento aleatorio, son llamados eventos seguros.Complementario : Cuando se considera un evento A, elevento que contiene todos los eventos elementales delespacio muestral que no estén en A se denominara EventoComplementario. Se simbolizara con Ā. Siempre quesumemos el evento A y su complemento Ā, tendremos elespacio muestral Ω (A + Ā = Ω). 10
11. Técnicas de Conteo Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar y que nos proporcionan la información de todas las maneras posibles en que ocurre un evento determinado. Permiten determinar el número de subconjuntos que se pueden obtener de un conjunto. Incluyen : las combinaciones, permutaciones y los diagramas de árbol. 11
12. Principio de conteo Multiplicativo Si se desea realizar una actividad que consta de r pasos, en donde:a) El primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas,b) el segundo paso de N2 maneras o formasc) y el n-ésimo paso de Nn maneras o formas,entonces esta actividad puede ser llevada a efecto de: N1 x N2 x ..........x Nn maneras o formas Cuando se trata de una sola actividad, la cual requiere para ser llevada a efecto de una serie de pasos, entonces haremos uso del principio multiplicativo 12
13. Principio de conteo Aditivo Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde:a) La primera de esas alternativas puede ser realizada de M maneras o formas,b) la segunda alternativa puede realizarse de N maneras o formas .....c) y la última de las alternativas puede ser realizada de W maneras o formas,entonces esa actividad puede ser llevada a cabo de: M + N + .........+ W maneras o formas Si la actividad a desarrollar o a ser efectuada tiene alternativas para ser llevada a cabo, haremos uso del principio aditivo. 13
14. Combinación Fórmula : COMBINACIÓN: Es todo arreglo de n!elementos en donde NO nCr =nos interesa el lugar o r!(n − r )!posición que ocupa cadauno de los elementos En donde, nCr = es el número de combinacionesque constituyen dicho de n objetos tomados r a la vez.arreglo, simplemente n! = factorial de nnos interesa formar (n-r)! = factorial de la diferencia entre n y rgrupos y su contenido. 14
15. Permutación Fórmula :PERMUTACIÓN: nEs todo arreglo de nPrelementos en donde SI n rnos interesa el lugar oposición que ocupa cada En donde,uno de los elementos que nPr = es el número deconstituyen dicho arreglo. permutaciones de n objetos tomados r a la vez. n! = factorial de n (n-r)! = factorial de la diferencia entre nyr 15
16. Probabilidad de eventosDos eventos A y B definidos en el mismo espacio muestral sonexcluyentes si NO PUEDEN OCURRIR JUNTOS. Es decir, la ocurrencia de uno EXCLUYE de la ocurrencia del otro. En símbolos si P (A ∩ B)= Ø P(A + B)= P(A) + P(B) Dos eventos A y B no son excluyentes si pueden ocurrir juntos. Es decir la ocurrencia de uno no excluye la ocurrencia del otro. En símbolos (A ∩ B) ≠ Ø P(A + B)= P(A) + P(B) – P(A ∩ B) 16
17. Probabilidad de eventosDos eventos A y B son dependientes, si un evento influyeen el otro evento. Observamos que el hecho de quesuceda el evento A influye en la probabilidad del suceso B,es decir la probabilidad del suceso B depende de que A sehaya realizado o no, esto se expresa como P (B/A). P(AB) = P (A) * P (B/A) Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). 17
18. Probabilidad de eventosSean A y B dos eventos asociados con un experimentoaleatorio. Consideremos que ya ocurrió el evento B yque p (B) > 0.Bajo estas condiciones se llama probabilidadcondicional de A dado B, y se escribe P (A/B), alcociente que se obtiene dividiendo la probabilidad dela intersección de A y B entre la probabilidad de B: P(A ∩ B) P (A /

CONCLUSIÓN

La estadística es una herramienta básica para negocios y producción. Es usada para entender la variabilidad de sistemas de medición, control de procesos así como el control estadístico de procesos, para compilar datos y tomar decisiones. En estas aplicaciones son herramienta clave y probablemente la única herramienta disponible. la estadística aplicada en ingeniería busca implementar los procesos probabilisticos y estadísticos de análisis e interpretación de datos o características de un conjunto de elementos al entorno industrial, a efectos de ayudar en la toma de decisiones y en el control de procesos industriales y organizacionales.

La importancia de la estadística e ingeniería se basa en la participación de la industria en el aumento de la calidad, ya que las técnicas estadísticas pueden emplearse para describir y comprender la variabilidad, que es el resultado de cambios en las condiciones bajo las que se hacen las observaciones